处理器微结构
现代处理器为了增加指令的吞吐,引入了指令流水线。相比单指令周期处理器,指令流水线将一条指令的执行过程划分为多个阶段,经典的5级流水线包括:取指(Instruction Fetch, IF)、译码(Instruction Decode, ID)、执行(Execution, EX)、访存(Memory, MEM)和写回(Write Back, WB) 5个阶段。指令流水线的每个阶段都有一套独立的硬件单元,因此在理想状态下,每个时钟周期每个阶段对应的硬件单元都能执行一次对应的操作,这样就形成了流水线,处理器每个时钟周期就可以完成一条指令的执行。图1展示了5级流水线指令执行过程,从第5个时钟周期开始,每个时钟周期都会完成一条指令的执行。
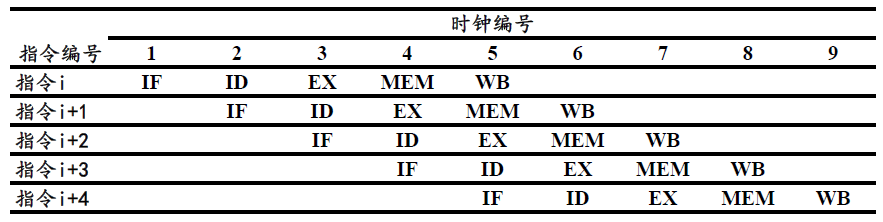
图1 5级流水线
但是,流水线在实际执行过程中不可能一直这样流畅的执行下去,会存在以下3种冒险,阻塞流水线:
结构冒险(Structural Hazard)
如果一条指令需要的硬件部分还在为之前的指令工作,而无法为这条指令提供服务,那就导致了结构冒险。
数据冒险(Data Hazard)
如果一条指令需要某数据而该数据正在被之前的指令操作,那这条指令就无法执行,从而导致了数据冒险。
控制冒险(Control Hazard)
如果现在要执行哪条指令,是由之前指令的运行结果决定,而现在那条之前指令的结果还没产生,就导致了控制冒险。
结构冒险(Structural Hazard)
由于指令流水化,处理器在同一个时钟周期,同时运行两条指令的不同阶段。但是这两个不同的阶段,可能会用到同样的硬件电路,如果硬件无法同时支持指令的所有可能组合方式,就会出现资源冲突,从而导致结构冒险。结构冒险本质上是硬件层面的资源竞争问题,可以通过增加硬件资源来解决。
典型的结构冒险的例子是内存的数据访问。由图1可知,在第$i$条指令执行到访存(MEM)阶段的时候,第$i+3$条指令正在执行取指(IF)的操作。访存和取指都要进行内存数据的读取,而内存只有一个地址译码器作为地址输入,这就意味着在一个时钟周期里内存只能读取一条数据,无法同时执行第$i$条指令的访存和第$i+3$条指令的取指操作。
一种解决方案是将内存分成存放指令的程序内存和存放数据的数据内存,每块内存拥有各自的地址译码器。这样把内存拆成两部分的解决方案,在计算机体系结构里叫做哈佛结构,而与此对应的则被称为冯·诺伊曼结构,又被称为普林斯顿架构。
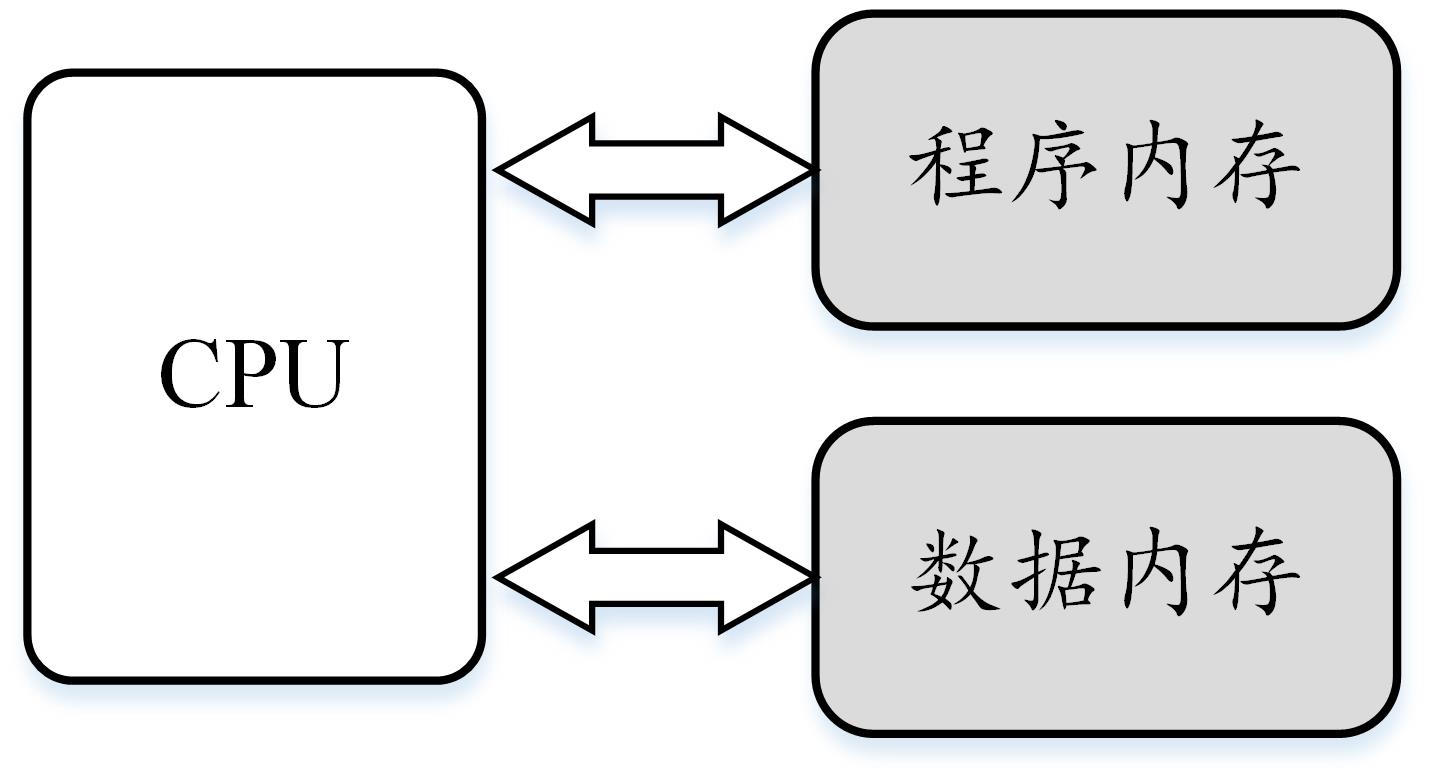 图2 哈佛结构 |
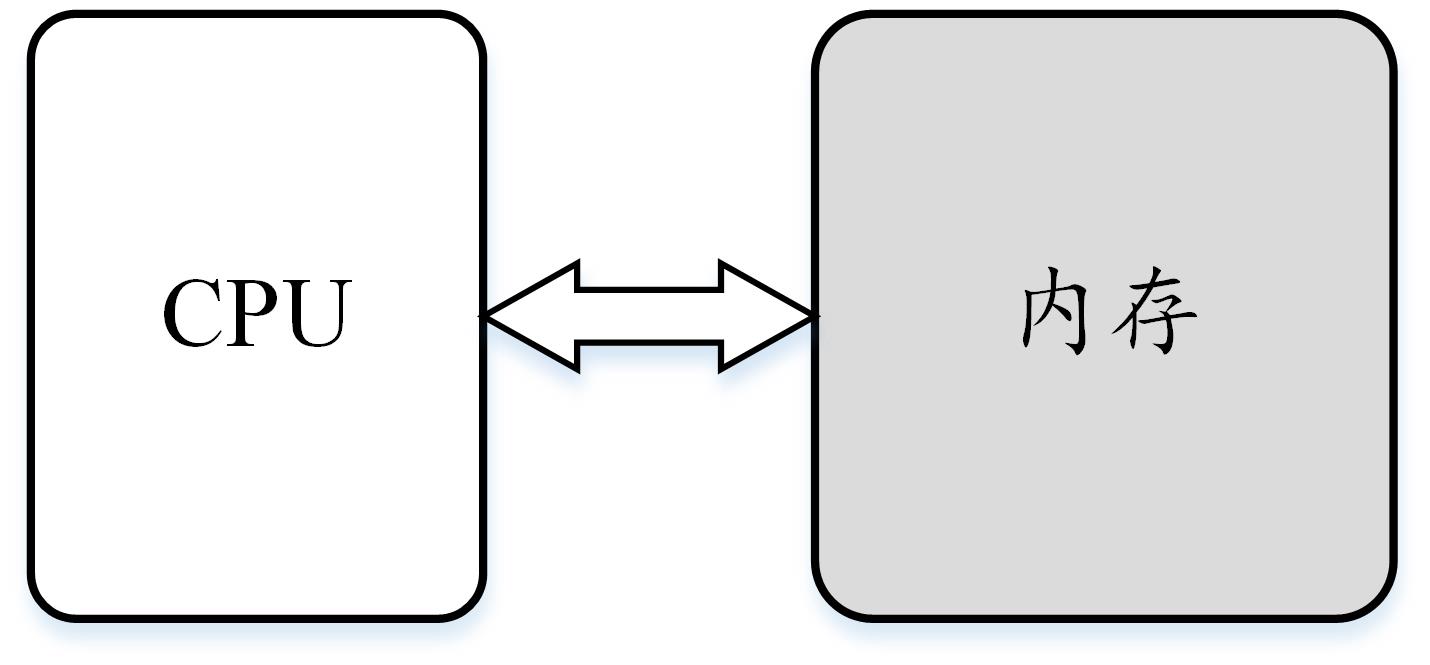 图3 冯诺依曼结构/普林斯顿结构 |
然而,虽然哈佛结构能够解决资源冲突问题,但是这为程序动态分配内存带来了挑战。因此,现代处理器依然采用冯·诺伊曼体系结构,同时借鉴了哈佛结构的思想,在处理器内部的高速缓存部分进行区分,把高速缓存分成了指令缓存(Instruction Cache)和数据缓存(Data Cache)两部分。
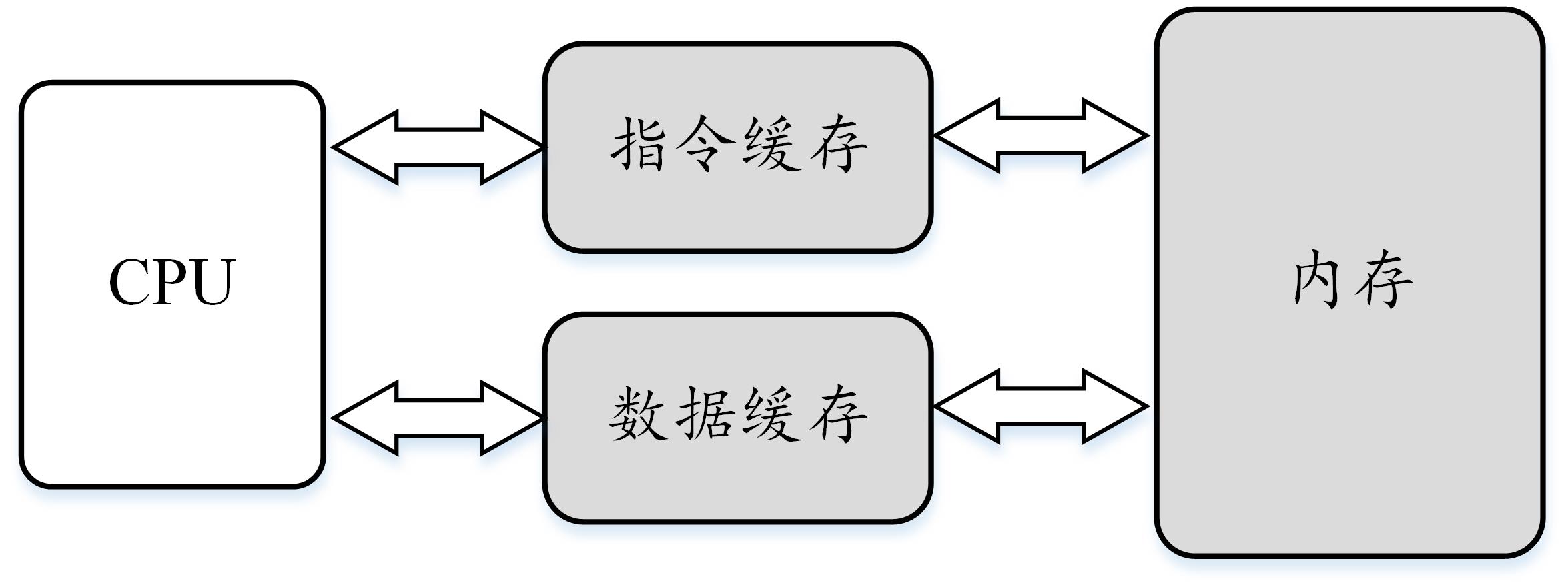
图4 现代处理器的混合结构
内存的访问速度远比处理器的速度慢很多,现代处理器并不会直接读取主内存,而是先从主内存把指令和数据加载到高速缓存中,然后直接访问高速缓存。指令缓存和数据缓存的拆分,使得处理器在进行访存和取值时,不会再发生资源冲突的问题。
数据冒险(Data Hazard)
处理器中对寄存器和内存的操作包括读取(Read)和写入(Write)等2种操作,这2种操作能够组合出4个操作序列:
先写后读(Read After Write, RAW)
上一条指令写入寄存器或内存,下一条指令读取写入数据,两条指令间存在
数据依赖(Data Dependency)关系,后一条指令需要等待上一条指令运行结束之后再运行。先读后写(Write After Read, WAR)
上一条指令读取寄存器或内存,下一条指令将新的数据写入同一个寄存器或内存,两条指令间存在
反依赖(Anti-Dependency)关系。写后再写(Write After Write, WAW)
两条指令前后写入同一个寄存器,两条指令间存在
输出依赖(Output Dependency)关系。读后再读(Read After Read, RAR)
两条指令前后读取同一个寄存器,无依赖关系。
除了读后再读,对于同一个寄存器或者内存地址的操作,其他3种操作序列都要求指令必须按照顺序执行。然而,指令流水线架构的核心,就是在前一个指令还没有结束的时候,开始执行后面的指令。如果一条指令的执行取决于先前指令的结果,就可能导致数据冒险。数据冒险的本质就是在同时执行的多个指令之间,存在数据依赖的情况。虽然WAR和WAW不是真正的数据相关,处理器可能会使用寄存器重命名来解决,但是尽量不要写出这样的数据相关。
消除数据冒险就是要消除指令之间的数据依赖,让前后指令之间不存在数据相关。解决数据冒险的一个简单方法就是流水线停顿(Pipeline Stall),又称流水线冒泡(Pipeline Bubbling)。在进行指令译码时,我们可以拿到指令所需要访问的寄存器和内存地址,从而就能够判断出来,这个指令是否会触发数据冒险,如果会触发数据冒险,我们可以让整个流水下停顿一个或多个周期。实际中并不是真的让流水线停下来,而是在执行后面的操作步骤之前,插入一个NOP操作,也就是执行一个什么也不做的操作。
控制冒险(Control Hazard)
分支指令及其他改变程序计数器的指令会改变指令的流向,因此转移指令本身和流水线的模式是冲突的,当对转移指令实现流水化时,可能导致控制冒险。转移指令大体分为:
直接转移:
j target无条件直接跳转指令的跳转地址在取指阶段就能得到,所以流水线不用停顿。
间接转移:
jr r0无条件间接跳转指令在
译码(ID)阶段得出跳转地址,流水线需停顿1个周期才能解决控制冒险。条件转移:
beq rs, rt, imm条件跳转指令需要根据
执行(EX)阶段的结果,判断是否跳转,需要等待2个周期。然而,实际上比较两个数是否相等十分简单,只需在译码(ID)阶段对寄存器的两个输出进行比较,从而可以将流水线停顿周期缩减为1个周期。
除了利用流水线停顿解决控制冒险,另外一种解决方法是延迟转移技术,其通过调整指令的顺序,将一定会执行的指令放在分支指令后面,这样流水线不会停顿。但是需要注意,调整指令顺序一定不能改变这段代码原来的意义。
流水线吞吐率
指令流水线将一条指令的执行过程划分为多个阶段,每个阶段的部件可同时执行多条指令的不同部分,从而提高各部件的利用率和指令的平均执行速度。流水线的吞吐率(Throughout Put rate, TP)是指单位时间内流水线所完成的任务数量或输出的结果数量,反映了指令的平均执行速度。计算流水线吞吐率的最基本公式如下:
通过消除指令间的结构冒险、数据冒险和控制冒险,可以测得指令的最大吞吐率 $TP_{max}$。通过消除指令间的结构冒险和控制冒险,但保留数据冒险,可以测得指令的最小吞吐率 $TP_{min}$。
最大吞吐率 $TP_{max}$ 反映了指令在不存在任何冒险的情况下的计算峰值,可用于评估程序优化空间。最小吞吐率 $TP_{min}$ 反映了指令在流水线失效情况下的计算延迟,可用于计算指令时钟周期。指令时钟周期计算公式为:
指令峰值和延迟
MegPeak 是旷视 MegEngine 团队开发的一款用于测试目标处理器指令的峰值带宽、指令延迟、内存峰值带宽和任意指令组合峰值带宽的工具,可帮助开发人员:
- 绘制 Roofline Model,指导开发人员优化模型性能
- 评估程序的优化空间
- 探索指令组合的理论计算峰值
有关进一步的介绍请移步Readme文档。
下面是 MegPeak 测试 Arm64 上 fmla 指令计算峰值的核心代码:
1 | static int fmla_throughput() { |
上面的内嵌汇编代码主要做了2件事:
- 初始化 0~19 号 NEON 寄存器为零,这一步不是必须的,但可以避免计算过程中出现 nan 导致的潜在影响;
- 创建主循环,主循环中执行
fmla指令,从对应的寄存器读取数据,并将计算结果写入到相同的寄存器中,同一条指令内部没有数据相关。
下面是 MegPeak 测试 Arm64 上 fmla 指令延迟的核心代码:
1 | static int fmla_latency() { |
上面的内嵌汇编代码中,将 fmla v0.4s, v0.4s, v0.4s\n 这条指令重复执行了 20 次,这样每条指令都依赖上一条指令的计算结果,所以存在严格的数据相关。通过统计执行时间和指令条数,可以计算出这条指令的计算延迟。