SM4-Sbox 结构
SM4-Sbox 查找表如图 1 所示。对于 S 盒的每 8 位输入,将前 4 位作为行,后 4 位作为列,输出即为查找表对应的元素。
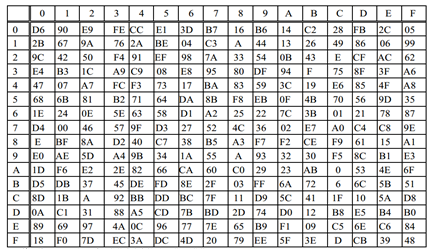
图 1 SM4-Sbox 结构
经过 LiuF 等人[1]的分析验证,SM4-Sbox 的代数表达式为:
其中,非线性运算 $I_{SM4}(x)$ 为有限域 $GF(2^8)$ 上的求逆运算,所用的素多项式为:
列向量 $C_{SM4}$ 为:
循环矩阵 $A_{SM4}$ 为:
对于 S 盒的 8 位输入 $x \in Z_2^8$ ,将其表示为 8 位列向量 $x = (x_0,x_1,x_2,x_3,x_4,x_5,x_6,x_7)^\mathrm{T}$ ,随后将其带入 S 盒代数表达式参与 $GF(2)$ 上的运算即可。
AES-Sbox 结构
AES-Sbox 查找表如图 2 所示。对于 S 盒的每 8 位输入,将前 4 位作为行,后 4 位作为列,输出即为查找表对应的元素。
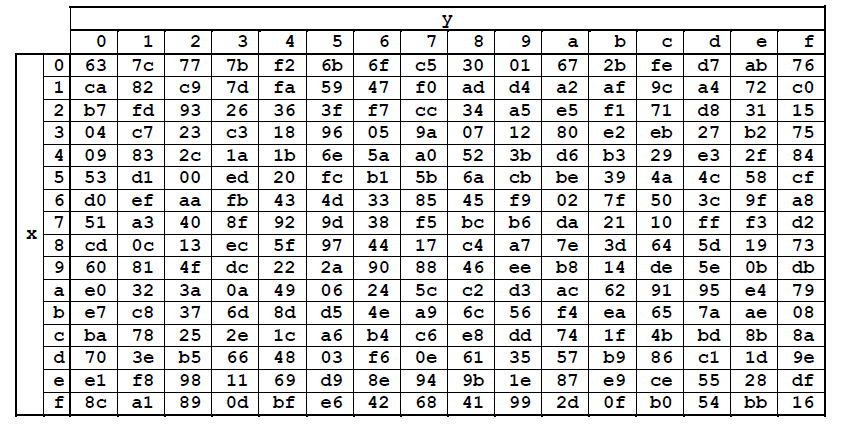
图 2 AES-Sbox 查找表
根据 AES 标准文档[2],AES-Sbox 的代数表达式为:
其中,非线性运算 $I_{AES}(x)$ 为有限域 $GF(2^8)$ 上的求逆运算,所用的不可约多项式为:
列向量 $C_{AES}$ 为:
循环矩阵 $A_{AES}$ 为:
SM4 与 AES 算法 S 盒的关系
由于 SM4 算法与 AES 算法的 S 盒均位于有限域 $GF(2^8)$ ,因此,两者的 S 盒存在某种映射关系,使得 SM4 算法与 AES 算法之间的 S 盒可以互相替换。
假设映射矩阵 $T_{S2A}$ 将 SM4 有限域中的元素映射到 AES 有限域中,那么根据 SM4-Sbox 的代数表达式,有:
注意上式是如何从第 2 步变换到第 3 步的,根据文献[1]可知,有限域中的求逆运算关于映射矩阵是同构的,因此把逆矩阵 $T_{S2A}^{-1}$ 从 $I_{SM4}$ 中提取出来后,此时求逆运算是在 AES 有限域上的元素进行运算的,因此在第 3 步中求逆运算由 $I_{SM4}$ 变成了 $I_{AES}$ 。
由 AES-Sbox 代数表达式可知:
将其带入公式 (3) 中,可得:
令
,则有:
至此,我们便得到了 SM4 与 AES 算法两者 S 盒的变换关系。